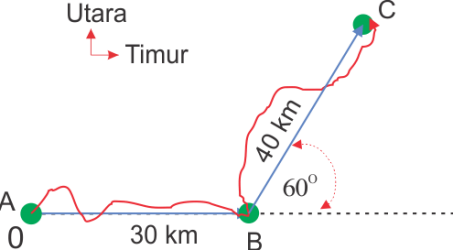
Menjumlahkan Dua Vektor Yang Mengapit Sudut
Halaman ini merupakan lanjutan dari halaman sebelumnya yang berjudul memahami cara penjumlahan vektor dimana halaman ini juga merupakan halaman keempat yang membahas tentang besaran vektor.
Nah, yang menjadi pembahasan saat ini adalah bagaimana jika dua buah vektor membentuk sudut sebesar Tetha?. Bagaimana cara menyelesaikannya?.
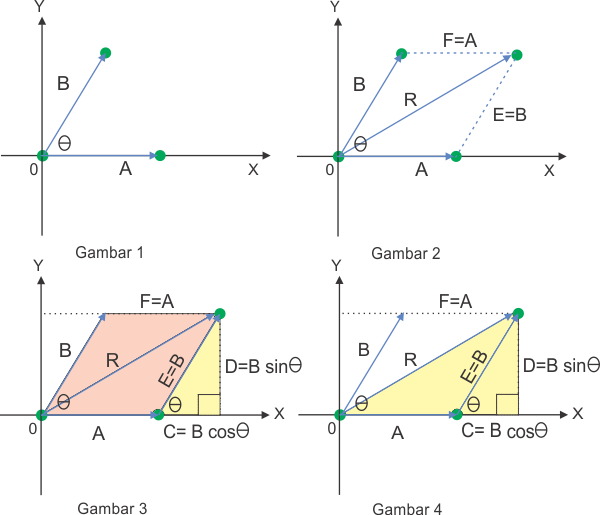
Cara menyelesaikannya yaitu dengan menggunakan metode jajargenjang yang kita buat seperti pada gambar 2. Dimana R merupakan resultan/hasil penjumlahan vektor A dan B.
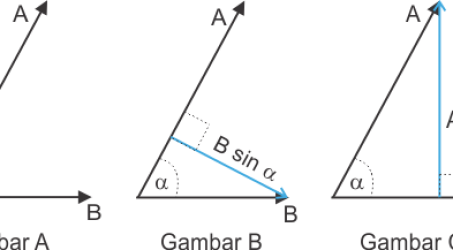
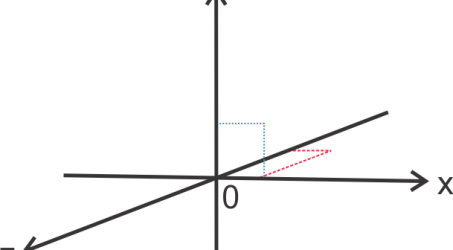
Jajargenjang pada gambar nomor 2 kemudian kita proyeksikan pada sumbu-x dan y sehingga menghasilkan garis C dan D (lihat nomor 3). Dimana nilai C = B cos ? dan D = B sin ?.
Sekarang perhatikan segitiga pada gambar 4 yang diberi warna kuning. Berdasarkan teorema Phytagoras, maka…
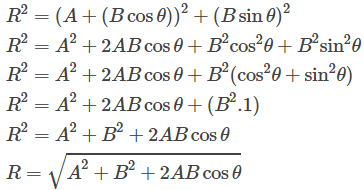
Sehingga besar resultan vektor |R| menjadi
![]()
Dimana |R| atau R merupakan besarnya resultan vektor yang bila membentuk sudut 90°, maka akan menjadi
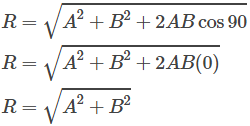
Rumus di atas pernah kita gunakan di halaman sebelumnya saat membahas tentang resultan dua vektor yang membentuk sudut 90° yaitu rumus teorema phytagoras.
Lalu bagaimana dengan rumus untuk menentukan arah vektor resultannya?
Perhatikanlah gambar di bawah ini
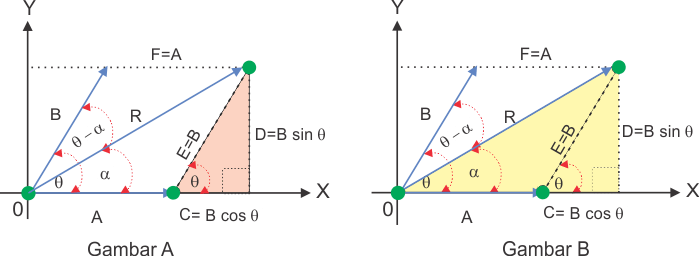
Dari segitiga merah pada gambar A diperoleh
![]()
Dari segitiga kuning pada gambar B diperoleh
![]()
Dari persamaan (1) dan (2) di atas, maka dapat kita peroleh
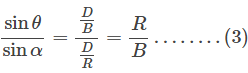
Persamaan (3) di atas dapat kita tuliskan menjadi
![]()
Rumus (4) di atas merupakan persamaan yang menghubungkan antara vektor B dan vektor resultan R. Lalu bagaimana hubungan vektor A dan vektor resultan R?. Simaklah pembahasan berikut ini.
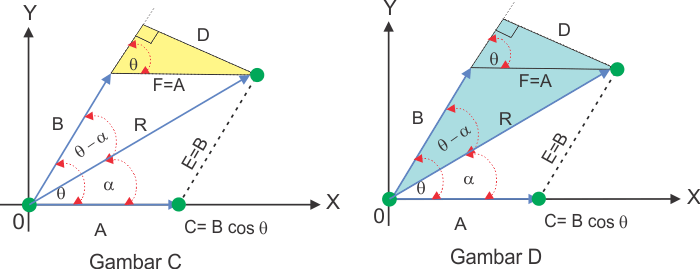
Dari segitiga kuning pada gambar C, diperoleh
![]()
Dari segitiga biru pada gambar D, diperoleh
![]()
Nah, dari persamaan (5) dan (6) diperoleh
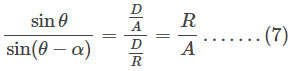
Persamaan (7) di atas dapat ditulis menjadi sebagai berikut
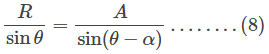
Persamaan (7) ini merupakan persamaan yang menghubungkan antara vektor A dan vektor resultan R. Untuk menghubungkan vektor A, vektor B dan resultan R, kita bisa melakukan penggambungan antara persamaan (4) dan persamaan (8) sehingga diperoleh:
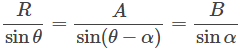
Nah, persamaan di atas ini merupakan rumus untuk menentukan arah vektor resultan.