Menguraikan Komponen Vektor
Setelah sebelumnya kita mempelajari cara menjumlahkan dua buah vektor, maka sekarang kita akan melakukan kebalikannya yaitu menguraikan komponen vektor dalam koordinat kartesius. Adapun untuk kepentingan praktis, kita menggunakan koordinat sumbu-x dan sumbu-y atau dua dimensi.
Contoh soalnya begini.
Ada sebuah mobil berjalan menuju arah timur laut dengan kecepatan 60 km/jam membentuk sudut 53° terhadap arah timur. Nah, tentukanlah komponen kecepatan mobil tersebut terhadap arah timur dan utara!
Jawab
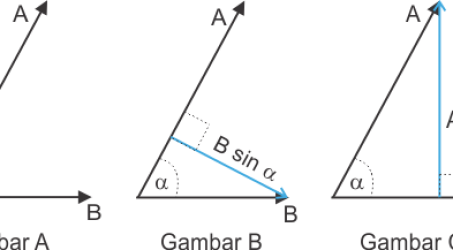
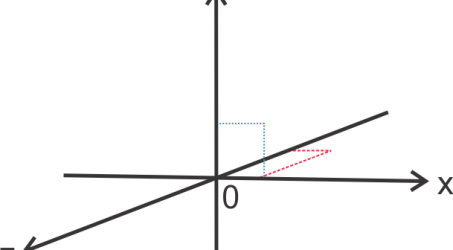
Untuk menguraikan komponen vektor hal yang paling mudah yaitu membuat gambarnya terlebih dahulu. Gambar ilustrasinya menjadi seperti di bawah ini
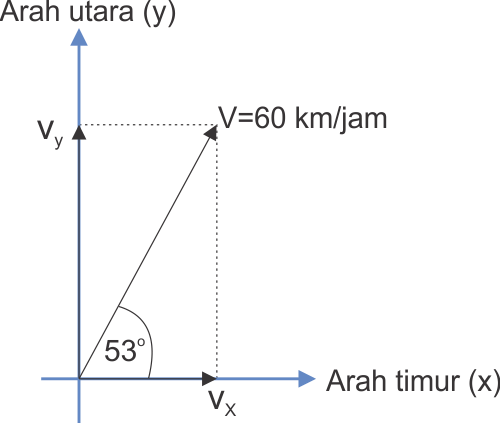
Dari gambar di atas, vx merupakan komponen kecepatan pada arah timur sedangkan vy merupakan komponen kecepatan pada arah utara.
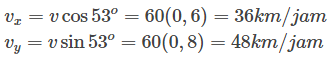
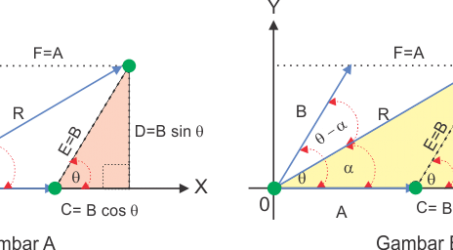
Dalam menguraikan komponen vektor entah itu satu buah vektor, dua buah vektor atau lebih caranya tetap sama seperti di atas yaitu vektor diproyeksikan kedalam sumbu-x dan sumbu-y. Namun untuk diingat bahwa jika terjadi pada minimal dua buah vektor, maka nanti akan ada resultan vektor sumbu x dan resultan vektor sumbu-y.
Untuk membaca halaman awal tentang besaran vektor bisa di lihat di sini.
Perhatikanlah gambar berikut ini
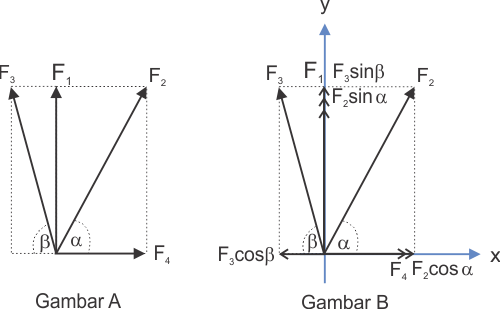
Pada gambar A, digambarkan bahwa ada empat buah vektor yang memiliki arah yang berbeda-beda yaitu F1,F2,F3 dan F4. Lalu ke-empat vektor tersebut bila di proyeksikan pada sumbu-x dan y, maka akan terlihat seperti pada gambar B. Nah, dari gambar B ini kita bisa melihat komponen vektornya.
Pada sumbu-x, resultan vektor komponennya yaitu
![]()
Nilai negatif (-) pada persamaan di atas menunjukan bahwa vektor tersebut berlawanan arah atau menuju nilai negatif.
Pada sumbu-y, resultan vektor komponennya yaitu
![]()
Lalu bagaimana dengan besar resultannya vektor (R)?, dapat kita gunakan persamaan teorema Phytagoras menjadi
![]()
Sedangkan untuk mengetahui ke arah mana vektor hasil penjumlahan, maka bisa menggunakan persamaan
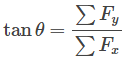
Untuk contoh penjumlahan dan penguraian vektor akan kita bahas pada halaman selanjutnya.