Di dalam fisika, terdapat dua jenis pengukuran yaitu pengukuran tunggal dan pengukuran berulang. Pengukuran tunggal adalah pengukuran yang dengan satu kali pengukuran langsung diperoleh hasil ukurnya berupa (x ± Δx) satuan dan jika dilakukan pengukuran berulang hasilnya tetap sama. Sedangkan pengukuran berulang adalah pengukuran dimana untuk mendapatkan hasil (x ± Δx) satuan harus dilakukan beberapa kali pengukuran karena disetiap kali pengukuran memperoleh hasil yang berbeda.
Pengukuran tunggal dan pengukuran berulang hasil ukurnya ditulis ke dalam bentuk (x ± Δx) dimana pada pengukuran tunggal nilai x merupakan angka pasti sebuah pengukuran dan Δx merupakan nilai ketidakpastiannya atau ralat. Sedangkan pada pengukuran berulang nilai x merupakan rata-rata perkiraan terbaik dari setiap pengulangan pengukuran dan Δx merupakan nilai ralat yang diperoleh dari nilai sebaran sekitar rata-rata atau standar deviasi.
A. Pengukuran Tunggal
Dalam pengukuran tunggal, penentuan hasil ukurnya tidak ada aturan tertentu (tidak harus ½ Nilai Skala Terkecil) dan hasil ukurnya ditentukan oleh keprofesionalitas si pengukur itu sendiri yang dilakukan secara logis dan rasional berdasarkan intuisi dan pemahaman yang dikuasainya.
Untuk contoh pengukuran tunggal Anda bisa membacanya pada artikel berjudul sistem pengukuran beserta alat ukur tentang pengukuran panjang benda menggunakan mistar. Di artikel tersebut dijelaskan bahwa penggunaan aturan ½ Nilai Skala Terkecil tidak bisa diterapkan disemua penguran alias tidak baku.
B. Pengukuran Berulang
Ada beberapa sebab mengapa sebuah pengukuran dilakukan secara berulang-ulang antara lain
- Adanya kesulitan eksperimen dalam pengulangan pengukuran
- Besaran yang diukur bersifat fluktuatif (berubah-ubah)
- Adanya variasi dari medium pada saat eksperimen dilakukan
Nah disini kita dapat menentukan angka pastinya dengan cara mengambil sejumlah data yang kemudian diambil nilai rata-ratanya. Sedangkan nilai ketidakpastiannya dapat diambil dari nilai deviasinya.
Nilai rata-ratanya dapat kita tentukan menggunakan persamaan di bawah ini:
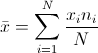Keterangan:
N merupakan jumlah data sedangkan ni merupakan banyaknya data xi yang muncul.
Untuk nilai deviasinya dapat kita tentukan dengan persamaan akar kuadrat dari ragam rerata sampel (averaged sample variance), yakni
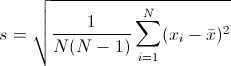
Dimana s merupakan standar deviasinya, N merupakan jumlah data, xi merupakan jumlah data ke-i dan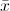 
merupakan nilai rata-ratanya.
Agar lebih mudah dalam perhitungan dan membuat Anda tidak bingung hendaknya data hasil pengukuran yang Anda lakukan dimasukan kedalam tabel.
