Pengertian dan Contoh Bilangan Heksadesimal

Dalam pelajaran teknik digital selain kita belajar tentang bilangan biner dan bilangan desimal, kita juga akan mempelajari tentang pengertian dan contoh bilangan heksadesimal.

Apa pengertian dan contoh bilangan heksadesimal itu? bagaimana cara merubah bilangan biner dan desimal ke bilangan heksadesimal? atau sebaliknya. Nah, di halaman ini kita akan membahas itu semua secara umum.

Pengertian bilangan heksadesimal

Bilangan heksadesimal merupakan bilangan yang memiliki 16 basis. Ingat! kalau bilangan desimal punya 10 basis sedangkan bilangan biner punya 2 basis.

Bilangan heksadesimal sering digunakan untuk memberi kode warna di dunia komputer, misalnya warna putih akan diberi kode warna #FFFFFF sedangkan warna warna hitam akan diberi kode warna #000000.

Contoh bilangan heksadesimal

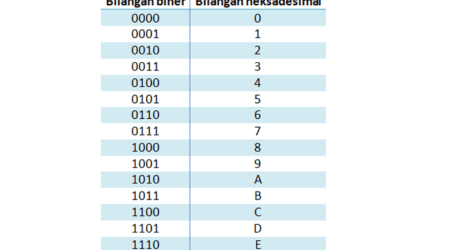
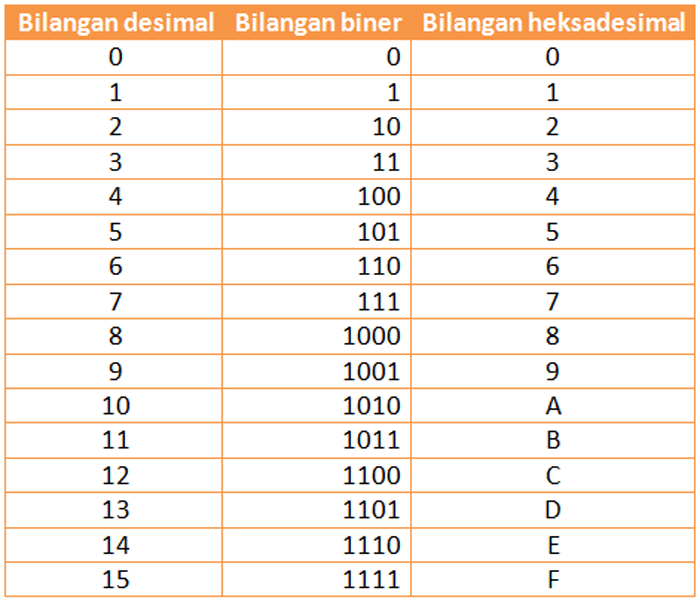
Contoh bilangan heksadesimal dengan 16 basisnya bisa dilihat di bawah ini.

Cara merubah bilangan desimal ke heksadesimal

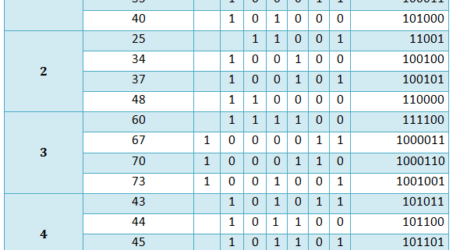
Untuk mengetahui cara merubah bilangan desimal ke heksadesimal, kita gunakan contoh-contoh soal. Biar lebih mahir hehehe

Artikel terkait: Contoh konversi biner ke desimal dan sebaliknya

Contoh 1:

Ubahlah bilangan desimal berikut 35, 420, 5500 dan 6060 ke dalam bilangan heksadesimal!

Jawab:

Perhitungannya berturut-turut sebagai berikut:

35/16 = 2 (3/16) -> sisa 3₁₀ = 3₁₆

2/16 = 0 -> sisa 2₁₀ = 2₁₆

sehingga 35₁₀ = 23₁₆

420/16 = 26 (4/16) ->  sisa 4₁₀ = 4₁₆

26/16 = 1 (10/16) -> sisa 10₁₀ = A₁₆

1/16 = 0 (1/16) -> sisa 1₁₀ = 1₁₀

sehingga 420₁₀ = 1A4₁₀

5500/16 = 343 (12/16) -> sisa 12₁₀ = C₁₆

343/16 = 21 (7/16) -> sisa 7₁₀ = 7₁₆

21/16 = 1 (5/16) -> sisa 5₁₀ = 5₁₆

1/16 = 0 (1/16) -> sisa 1₁₀ = 1₁₆

sehingga 5500₁₀ = 157C₁₆

6060/16 = 378 (12/16) -> sisa 12₁₀ = C₁₆

378/16 = 23 (10/16) -> sisa 10₁₀ =A₁₆

23/16 = 1 (7/16) -> sisa 7₁₀ = 7₁₆

1/16 = 0 (1/16) -> sisa 1₁₀ = 1₁₆

sehingga 6060₁₀ = 17AC₁₆

Contoh 2:

Tiga buah bilangan desimal ditulis berturut-turut sebagai berikut ini: 1350, 4000 dan 8875. Bagaimana penulisan ketiga bilangan desimal tersebut ke dalam bilangan heksadesimal?

Jawab:

Cara yang kita gunakan masih sama dengan contoh sebelumnya yakni:

1350/16 = 84 (6/16) -> sisa 6₁₀ = 6₁₆

84/16 = 5 (4/16) -> sisa 4₁₀ = 4₁₆

5/16 = 0 (5/6) -> sisa 5₁₀ = 5₁₆

sehingga 1350₁₀ = 546₁₆

4000/16 = 250 (0/16) -> sisa 0₀ = 0₀

250/16 = 15 (10/16) -> sisa 10₁₀ = A₁₆

15/16 = 0 (15/16) -> sisa 15₁₀ = E₁₆

sehingga 4000₁₀ = FA0₁₆

8875/16 = 554 (10/16) -> sisa 10₁₀ = A₁₆

554/16 = 34 (10/16)-> sisa 10₁₀ = A₁₆

34/16 = 2 (2/16) -> sisa 2₁₀ = 2₁₀

2/16 = 0 (2/16) -> sisa 2₁₀ = 2₁₀

sehingga 554₁₀ = 22A₁₆

Cara merubah bilangan heksadesimal ke desimal

Untuk memahami cara merubah atau mengkonversi bilangan heksadesimal ke desimal bisa lebih mudah bila melihat contohnya berikut ini.

Contoh

Ubahlah bilangan heksadesimal berikut 23, 1A4, 157C dan 17AC menjadi bilangan desimal!

Jawab

Untuk menjawab soal konversi heksadesimal ke desimal di atas bisa dilihat pada perhitungan berturut-turut berikut:

23₁₆ = (2×16¹) + (3×16⁰) = 32 + 3 = 35₁₀

1A4₁₆ = (1×16²) + (10×16¹) +(4×16⁰) = 256 + 160 + 4 = 420₂

157C₁₆ = (1×16³) + (5×16²) + (7×16¹) + (12×16⁰) = 4096 + 1280 + 112 + 12 = 5500₁₀

17AC₁₆ = (1×16³) + (7×16²) + (10×16¹) + (12×16⁰) = 4096 + 1792 + 160 + 12 = 6060₁₀

Daftar Pustaka

Dokumen pribadi, mata kuliah teknik digital.