Pada artikel yang lalu, kita telah mempelajari tentang konversi bilangan desimal ke heksadesimal begitu sebaliknya, maka pada halaman ini kita bahas tentang konversi bilangan biner ke heksadesimal dan sebaliknya.

Seperti biasa, untuk memahami cara konversi bilangan kita langsung praktek menggunakan contoh-contoh soal dan pembahasannya. Untuk itu perhatikanlah baik-baik, dan apabila belum paham, maka bisa bertanya di kolom komentar.

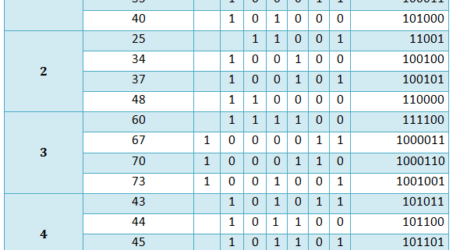
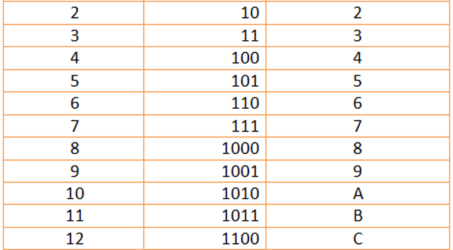
Sebelum membahas lebih jauh, perhatikan dulu tabel hubungan bilangan biner dan heksadesimal berikut ini.

A. Konversi bilangan biner ke heksadesimal

Untuk merubah bilangan biner ke heksadesimal, maka dapat dilakukan dengan cara mengelompokkan menjadi 4 bit tiap satu kelompok.

Misalnya: 11101100 kita pisahkan menjadi (1110) (1100)

Kemudian baru dikonversi menjadi

(1110) = E dan (1100) = C

Jadi diperoleh 11101100₂ = EC₁₆

Pertanyaan selanjutnya, bagaimana bila bilangan binernya hanya berjumlah kurang dari 4 bit?

Jika seperti ini, maka kita dapat menambahkannya dengan angka 0 di sisi paling kiri sehingga menjadi berjumlah 4 bit.

Misalnya:

1₂ = …..₁₆ ?

Kita bisa menambahkan angka 0 sehingga menjadi

0001₂ = 1₁₆

atau contoh lainnya;

110₂

Kita tambah angka 0 sehingga menjadi

0110₂ = 6₁₆

Contoh lain:

Ubahlah bilangan biner berikut menjadi bilangan heksadesimal. Bilangan tersebut yaitu: 011, 101101 dan 11110001.

Jawabannya:

a) 011₂ = 0011₂ = 3₁₆

b) 101101 = (0010) (1101) = 2D₁₆

c) 11110001 = (1111) (0001) = F1₁₆

Sangat mudah bukan? kalau sudah faham cara di atas, maka kita kasih contoh bilangan biner yang lebih panjang.

Artikel terkait: Pengertian dan contoh bilangan heksadesimal

Ubahlah bilangan biner ini menjadi penulisan bilangan heksadesimal:

1010110100101001₂

Jawabannya:

1010110100101001₂ = (1010) (1101) (0010) (1001)

1010110100101001₂ = AD29₁₆

Contoh satu lagi;

Tolong ubah bilangan biner 1101011010110₂ menjadi bilangan heksadesimal dengan benar!

Jawab:

1101011010110₂ = (0001) (1010) (1101) (0110) = 1AD6₁₆

B. Konversi bilangan heksadesimal ke biner

Cara mengubah bilangan heksadesimal ke biner dapat dilakukan dengan cara memisahkan setiap bilangan heksadesimal kemudian merubah setiap angkanya menjadi 4 buah bit.

Ini merupakan langkah kebalikan dari yang telah kita bahas di atas. Untuk lebih mudahnya perhatikanlah contoh-contoh berikut ini berturut-turut:

a) 4F73, b) 7AD1, c) 54A1, d) 37C843, e) 11276A7, f) 34762CB, g) AB277, h) 1DF17, i) 11A89 dan j) 875BA1

Jawab:

a) 4F73 = (0100) (1111) (0111) (0011)

Jadi angka 4F73₁₆ = 0100111101110011₂

b) 7AD1 =  (0111) (1010) (1101) (0001)

Jadi angka 7AD1₁₆ =  0111101011010001₂

c) 54A1 = (0101) (0100) (1010) (0001)

Jadi angka 54A1₁₆ = 0101010010100001₂

Artikel terkait: Contoh konversi biner ke desimal dan sebaliknya

d) 37C843 = (0011) (0111) (1100) (1000) (0100) (0011)

Jadi angka 37C843₁₆ = 001101111100100001000011₂

e) 11276A7 = (0001) (0001) (0010) (0111) (0110) (1010) (0111)

Jadi angka 11276A7₁₆ = 0001000100100111011010100111₂

f) 34762CB = (0011) (0100) (0111) (0110) (0010) (1100) (1011)

Jadi angka 34762CB₁₆ = 0011010001110110001011001011₂

g) AB277 = (1010) (1011) (0010) (0111) (0111)

Jadi angka AB277₁₆ = 10101011001001110111₂

Artikel terkait: Bilangan biner dan bilangan desimal

h) 1DF17 = (0001) (1101) (1111) (0001) (0111)

Jadi angka 1DF17₁₆ = 00011101111100010111₂

i) 11A89 = (0001) (0001) (1010) (1000) (1001)

Jadi angka 11A89₁₆ = 00010001101010001001₂

j) 875BA1 = (1000) (0111) (0101) (1011) (1010) (0001)

Jadi angka 875BA1₁₆ = 100001110101101110100001₂

Demikianlah cara dan contoh konversi bilangan biner ke heksadesimal atau konversi bilangan heksadesimal ke biner. Apabila ada pertanyaan bisa di ketik di kotak komentar.

Daftar Pustaka:

Dokumen pribadi mata kuliah Teknik Digital.